To answer my own question, the first module to be defined appears to be the root module. So I needed to start the specification with BinarySearch.tla not the context module (even though the dependency is the other way). Any hints on how to improve on the specifications still appreciated.
Jonathan
=============================
I have written a binary search algorithm with two modules as shown below. Both modules appear to parse and the BinarySearch seems to translate without errors.
\* BEGIN TRANSLATION …. …. ….
Spec == /\ Init /\ [][Next]_vars
/\ WF_vars(Next)
Termination == <>(pc = "Done")
\* END TRANSLATION
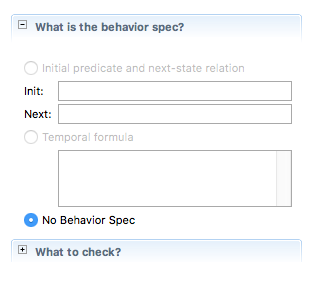
However, when selecting TLC-Model-Checker —> new Module, the No Behaviour-Spec button is selected, and the Temporal Formula button cannot be selected for Spec. So I cannot check the model.
This has not happened with other algorithms so I am wondering what I did wrong?
(Also, any help on writing the specifications for this algorithm would be appreciated).
Thanks
Jonathan
===============

------------------------ MODULE BinarySearchContext ------------------------
EXTENDS Sequences, Integers
IsSorted(s) == \A i,j \in DOMAIN s: i <= j => s[i] <= s[j]
SortedSeq(s) == { seq \in Seq(s) : IsSorted(seq) }
Range(f) == { f[x] : x \in DOMAIN f }
SortedSeqN(s,N) == UNION { { seq \in [ 1..n -> s ] : IsSorted(seq) } : n \in 1..N }
N == 7
Vals == 0..N+1
SmallSortedS == { seq \in SortedSeqN(1..N,N) : seq[1] = 1 }
=============================================================================
PlusCal options (-termination)
---------------------------- MODULE BinarySearch ----------------------------
EXTENDS BinarySearchContext, Integers, TLC
(***************************************************************************
--algorithm BinarySearch
variables
f \in SmallSortedS
, v \in Vals \* target
, p = 1, q = Len(f)
, mid = -2
, r = 0
, found = FALSE
begin
if v <= f[q] then
while p <= q /\ ~found do
mid := (p+q) \div 2;
if v = f[mid] then
r := mid[f];
found := TRUE;
elsif v > f[mid] then
p := mid + 1
else
q := mid - 1
end if;
end while;
end if;
print v;
assert (v \in Range(f) => r \in DOMAIN f /\ f[r] = v) ;
assert (r = 0 <=> ~ v \in Range(f)) ;
end algorithm
***************************************************************************)