Re: [tlaplus] on tlaps semantics

четверг, 24 марта 2022 г. в 19:00:09 UTC+3, Stephan Merz:

Hello,

for me both of your theorems are proved (by the SMT backend). Can you use SMT to prove simple theorems such as

THEOREM
ASSUME NEW x \in Int
PROVE x+1 = 1+x
OBVIOUS

or do you perhaps have a problem with your TLAPS installation?

Regards,
Stephan

On 24 Mar 2022, at 16:45, Алексей Тимаков <timako...@xxxxxxxxx> wrote:

Hi all

Can anyone tell me why this assumption cannot be proved.

THEOREM TEST4 == ASSUME NEW P1, NEW P2, NEW pred1 (_,_), NEW l, NEW pred2(_),
l = {x \in {pred1(c1, c2) : c1 \in P1, c2 \in P2} : pred2(x)}
PROVE \A l1 \in l : \E s1 \in P1, s2 \in P2 : l1 = pred1(s1, s2)
PROOF OBVIOUS
or even

THEOREM TEST2 == ASSUME NEW P1, NEW P2, NEW pred1 (_,_), NEW l,
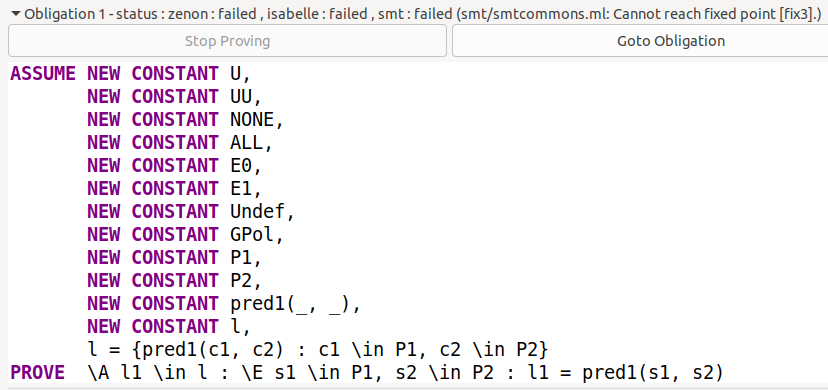
l = {pred1(c1, c2) : c1 \in P1, c2 \in P2}
PROVE \A l1 \in l : \E s1 \in P1, s2 \in P2 : l1 = pred1(s1, s2)
PROOF OBVIOUS
Thanks.

--
You received this message because you are subscribed to the Google Groups "tlaplus" group.
To unsubscribe from this group and stop receiving emails from it, send an email to tlaplus+u...@xxxxxxxxxxxxxxxx.
To view this discussion on the web visit https://groups.google.com/d/msgid/tlaplus/bd3b0337-27ab-40e7-9eef-faf5d4c34256n%40googlegroups.com.