you can also try using our ProB validation tool.
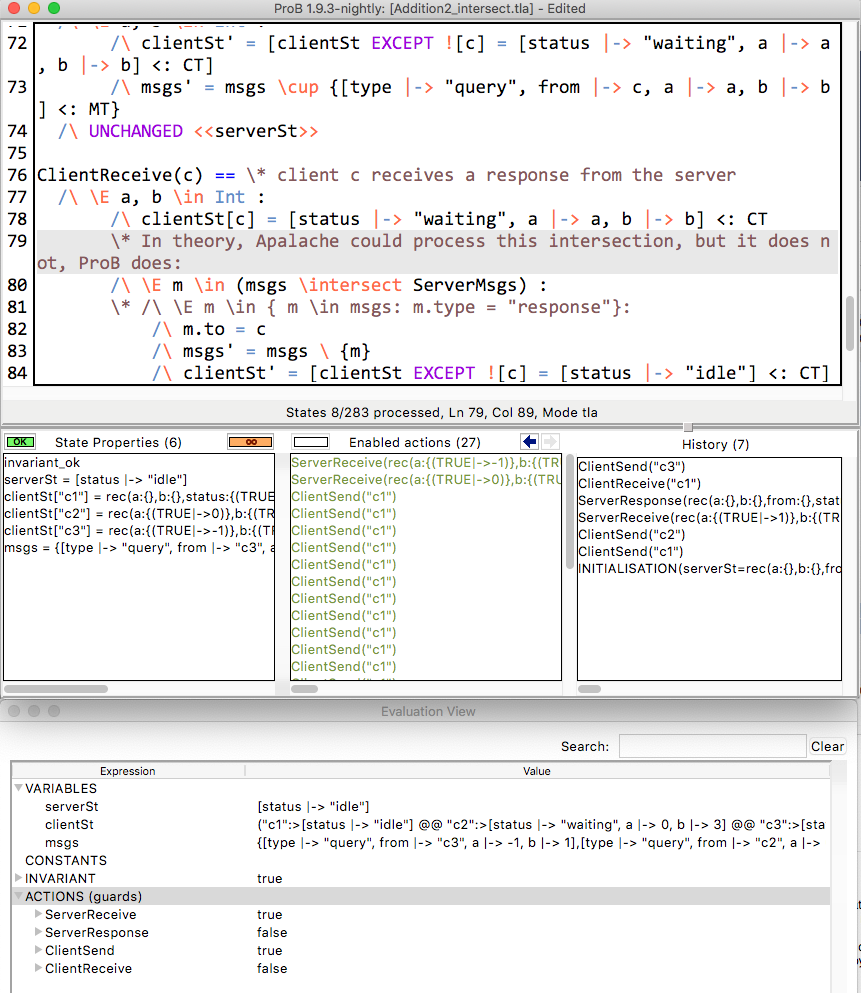
It can handle Addition2.tla that Igor sent. It can also deal with the commented out version of the existential quantifier without filter set:
\E m \in (msgs \intersect ServerMsgs); see the screenshot below.
(Note: The orange infinity symbol states that not all transitions for ClientSend were computed due to an unbounded quantification.)
ProB, however, requires that its type inference can infer a type for all variables.
The original Addition.tla from Abel raises a type error.
The TLA mode would also benefit from making it more accessible to persons not familier with B (the TLA models are translated to the
B language, and this shines through in various places in the tool).
Greetings,
Michael
On 4 Feb 2020, at 16:13, Igor Konnov <igor.konnov@xxxxxxxxx> wrote:
Hi Abel,
Depending on the properties that you like to check, you might want to try the Apalache model checker [1]. Although the theory and the tool are not that mature as with TLC, Apalache can handle existential quantifiers over Int and Nat, as long as the checker can replace a quantifier with an integer constant. As long as the model checker has to reason about finite sets, even though their elements may be integers, it should work.
I have added tool-specific type annotations in your specification and replaced an infinite set of records with a set filter in ClientReceive, so apalache could digest the spec. (Stephan already mentioned the issue with “idle”, which I have replaced with [status |-> “idle”].) The next question is the kind of property you like to check. At the moment, we can check inductive invariants and safety, by unrolling the transition relation.
[1] https://github.com/konnov/apalache/tree/unstable
Best regards,
Igor
You received this message because you are subscribed to the Google Groups "tlaplus" group.
To unsubscribe from this group and stop receiving emails from it, send an email to tlaplus+unsubscribe@xxxxxxxxxxxxxxxx.
To view this discussion on the web visit https://groups.google.com/d/msgid/tlaplus/631B29BF-F81D-45ED-99FC-F0DECD64A141%40gmail.com.